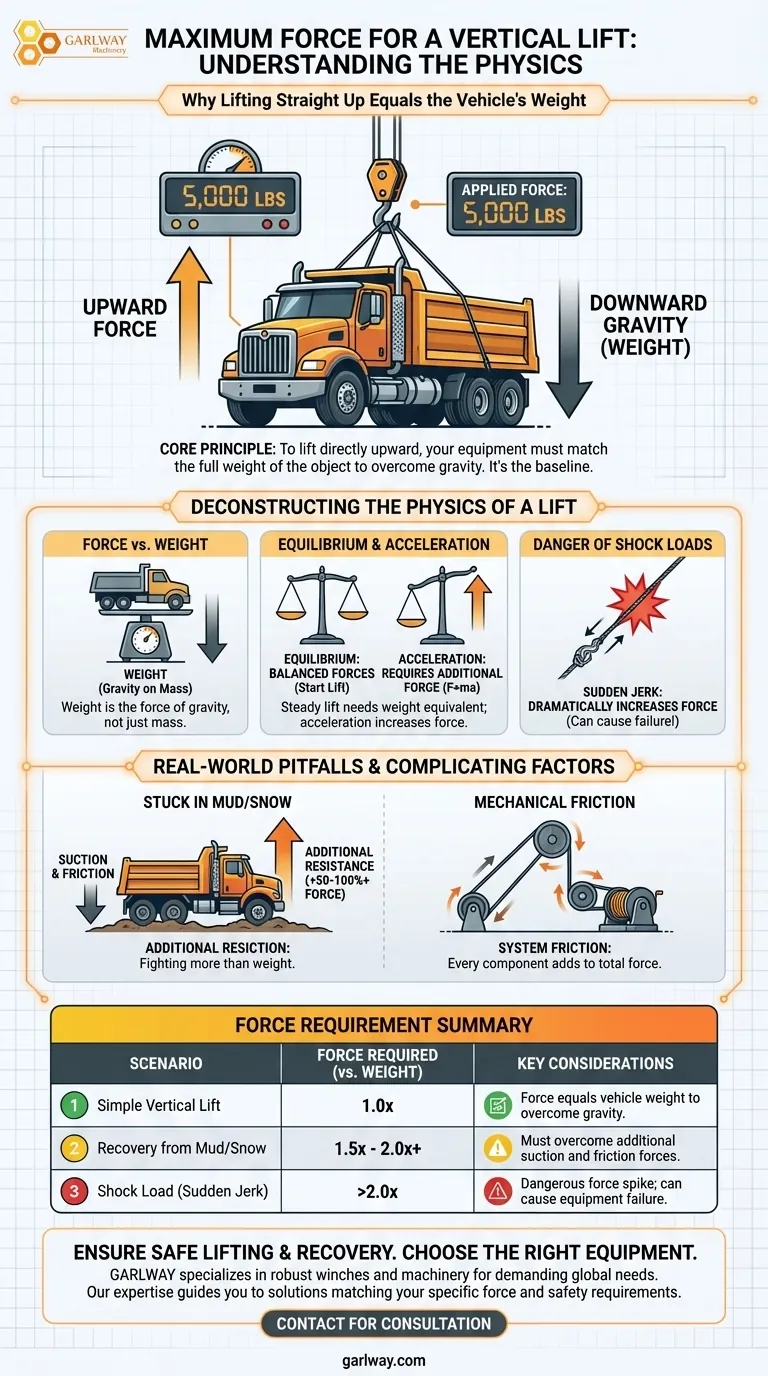
In the simplest terms, the maximum force required to pull a vehicle straight upward is equal to the vehicle's own weight. If a truck weighs 5,000 pounds, you need to apply 5,000 pounds of force directly upward just to lift it off the ground.
To overcome the force of gravity in a direct vertical lift, your equipment must be capable of matching the full weight of the object. This is a fundamental principle of physics that forms the baseline for any lifting or recovery calculation.

Deconstructing the Physics of a Vertical Lift
Understanding why the required force equals the vehicle's weight is crucial for safe and effective operation. This isn't just a rule of thumb; it's a direct application of core physics principles.
Force vs. Weight: The Core Relationship
A vehicle's weight is the specific measurement of the force of gravity acting on its mass. It is not the same as mass itself.
When you lift a vehicle, you are applying an upward force to counteract the downward force of gravity (its weight).
The Concept of Equilibrium
To begin the lift, you must apply a force that is at least equal to the vehicle's weight. This creates a state of equilibrium, where the upward force and the downward force (gravity) are balanced.
To achieve actual upward movement, the force applied must be infinitesimally greater than the vehicle's weight. For all practical calculations regarding equipment capacity, we consider the maximum required force to be 1.0 times the vehicle's weight.
The Critical Role of Acceleration
Newton's Second Law (Force = Mass × Acceleration) tells us that any upward acceleration requires additional force.
Lifting a vehicle slowly and steadily requires a force equal to its weight. However, jerking the line or trying to lift it quickly will dramatically increase the force required, creating a dangerous "shock load."
Common Pitfalls and Complicating Factors
While the physics of a simple vertical lift are straightforward, real-world scenarios are rarely perfect. Several factors can increase the force required well beyond the vehicle's curb weight.
The Danger of Shock Loads
A sudden pull or a "running start" on a recovery line can multiply the force exerted on the system. This shock load can easily exceed the working load limit of winches, ropes, and connection points, leading to catastrophic failure.
Resistance from Being Stuck
If a vehicle is stuck in mud, sand, or snow, you are fighting more than just its weight. You must also overcome the powerful forces of suction and friction.
This additional resistance can easily add 50% to 100% (or more) to the force required for extraction compared to a simple lift.
Mechanical Friction in Your System
Every pulley, block, or change in direction in your rigging setup introduces friction. While often minor, this friction adds to the total force your winch or lifting mechanism must generate to move the load.
Making the Right Choice for Your Task
Use this understanding of force to select the right equipment and strategy. Your primary goal dictates how you should interpret the "1.0x vehicle weight" rule.
- If your primary focus is a simple, controlled vertical lift: Your equipment (crane, winch, etc.) must have a working load limit rated for at least the full weight of the vehicle.
- If your primary focus is recovery from mud or snow: Assume the required force will be significantly higher than the vehicle's weight and use equipment with a substantial safety factor (e.g., a winch rated for 1.5x to 2.0x vehicle weight).
- If your primary focus is safety in any scenario: Always operate slowly and smoothly to avoid shock loading your equipment.
Understanding this fundamental principle empowers you to plan your operations safely and effectively.
Summary Table:
| Scenario | Force Required (vs. Vehicle Weight) | Key Considerations |
|---|---|---|
| Simple Vertical Lift | 1.0x | Force equals vehicle weight to overcome gravity. |
| Recovery from Mud/Snow | 1.5x - 2.0x+ | Must overcome additional suction and friction forces. |
| Shock Load (Sudden Jerk) | >2.0x | Dangerous force spike; can cause equipment failure. |
Ensure Your Lifting and Recovery Operations are Safe and Effective
Choosing the right equipment is critical. The force calculations in this article are fundamental to selecting winches and other machinery with the appropriate capacity and safety margins.
GARLWAY specializes in providing robust construction machinery, including powerful winches, concrete mixers, and batching plants, designed for the demanding needs of construction companies and contractors globally.
Let our expertise guide you to the right solution. Contact our team today for a consultation on equipment that matches your specific force and safety requirements.
Visual Guide
Related Products
- Electric and Hydraulic Winch for Heavy Duty Applications
- Portable Small Trailer Winch
- Warn Winch Windlass Boat Trailer Winch
- Small Electric Winch 120V and 240V for Compact Applications
- 12000 lb Heavy Duty Electric Boat Winch
People Also Ask
- Can an electric winch be used as a hoist? Understand the Critical Safety Differences
- Can you use an electric winch manually? A Guide to Dual-Functionality Winches
- How is an electric winch powered? Unlock the Power Conversion System for Heavy Lifting
- How to maintain an electric winch? Ensure Peak Performance & Reliability for Your Projects
- How to power an electric winch on a trailer? Choose the Best Method for Your Setup



















